最新のテストの解説・難易度分析は以下の記事よりご覧下さい。
※振替日程や全ての部の試験実施日時を調査の上、全てのテスト終了後に配信しております。コベツバでは、2025年12月7日実施、サピックス6年生 第4回合格力判定サピックスオープンの平均点・算数解説・難易度・所感を公開中です。[…]
※振替日程や全ての部の試験実施日時を調査の上、全てのテスト終了後に配信しております。
志望校判定サピックスオープンの平均点・分析・今後の対策などの詳細につきましては、以下の記事をご覧下さい。
▼4年〜5年の方はこちらへ【サピックス4年生・5年生】実力診断・志望校診断サピックスオープン(SO)の概観/平均点/分析/対策▼サピックスオープン解説はこちら(テストが近づけば、最新版の記事をご覧になれます)志望校診断サピ[…]
コベツバでは、2022年6月12日実施、第2回志望校判定サピックスオープンの算数解説・難易度・所感を公開中です。
第2回志望校判定サピックスオープンの過去の平均点
過去4年間の4科目平均点は以下の通りです。満点が普段の倍(4科目1000点 / 算数300点)になっています。
| 平均点 | 偏差値60ライン(≒アルファクラス基準) | |
| 4科合計 | 479点(47.9%) | 593.8点(59.4%) |
| 算数 | 119.4点(39.8%) | 170.3点(56.8%) |
過去2年間の「A:技術」の平均点は以下の通りです(満点:4科目500点 / 算数150点)。
| 平均点 | 偏差値60ライン(≒アルファクラス基準) | |
| 4科合計 | 284.2点(56.8%) | 349.3点(69.9%) |
| 算数 | 69.1点(46.1%) | 97.5点(65%) |
過去2年間の「B:思考力」の平均点は以下の通りです(満点:4科目500点 / 算数150点)。
| 平均点 | 偏差値60ライン(≒アルファクラス基準) | |
| 4科合計 | 212.7点(42.5%) | 273.1点(54.6%) |
| 算数 | 51.1点(34.1%) | 78.6点(52.4%) |
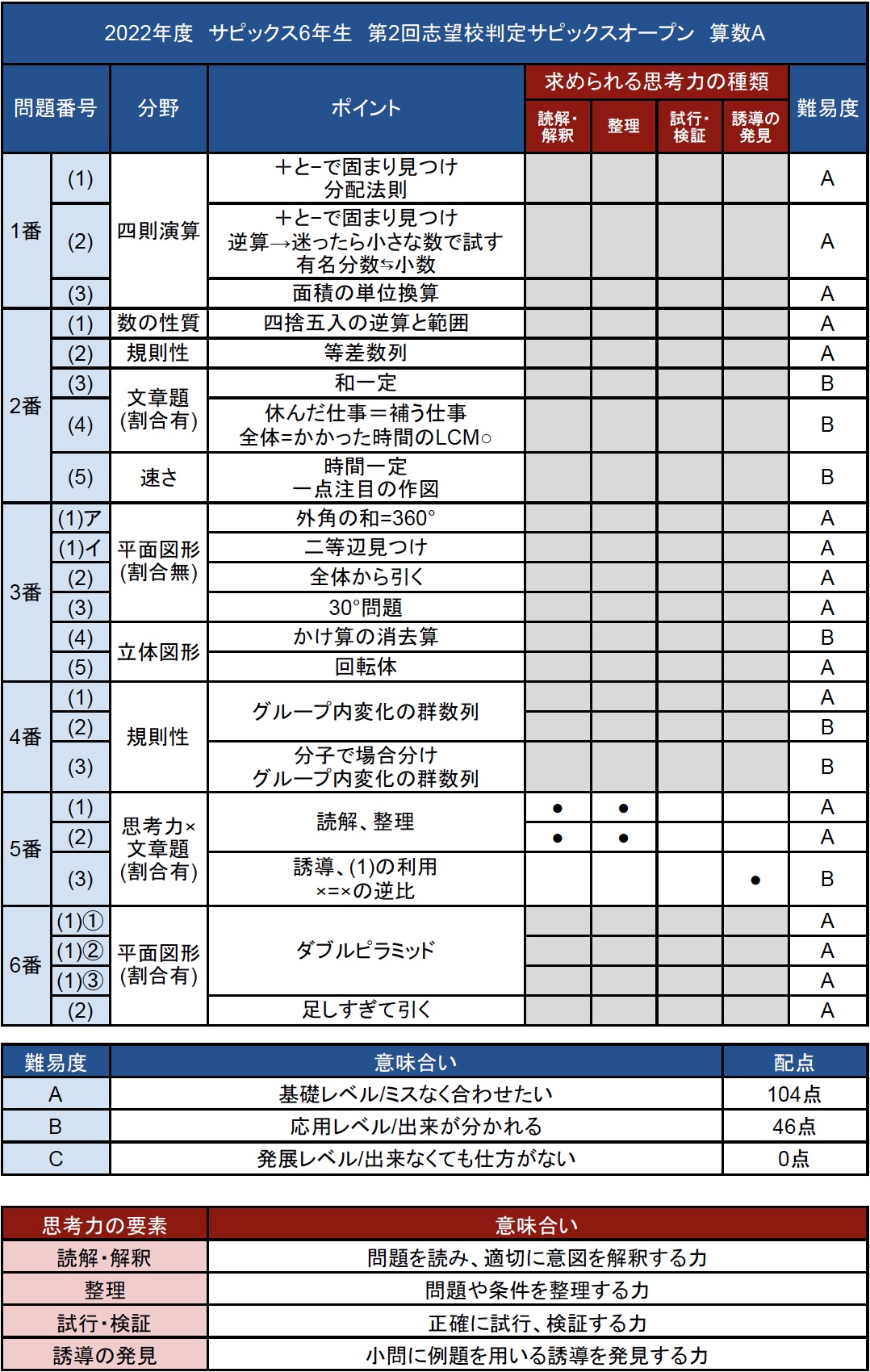
<算数A>第2回志望校判定サピックスオープンの難易度・所感
第2回志望校判定サピックスオープン(SO)の【算数A】です。
全体感としてはレベルAが約7割、残りがレベルBということで標準的な難易度構成となりました。
算数Aと算数Bを分けている為、当然ながら技術系中心の出題がメインとなりました。
解きにくい部分があったとすれば、通常のマンスリーや組分けよりも大問2番に複数レベルBの問題が入っていたことで、それによってペースを崩されてしまった人が一定数出たのではないかと想像します。
以下、レベル Bの問題に対してコメントしておきます。
■2番(3):和一定
はじめの状態から2パターンのやりとりということで、整理の方法に気を付けて和一定に気づくことが出来ればおしまいです。
■2番(4):休んだ仕事=補う仕事、全体=かかった時間のLCM○
図を書いて整理していくだけでも解くことが出来ますが、休んだ仕事=補う仕事の考え方できれいに解くことができる問題でした。
■2番(5):時間一定、一点注目の作図
複数の列車が同時に出現する通過算では、同時記号の扱いと時間一定を使って解くことが出来ます。
一点注目で学習した考え方をベースに記号を使って旅人算に転換できると簡単になります。
■3番(4):かけ算の消去算
かけたり割ったりすることで必要なものを求めるという判断をすることができるかが問われました。
■4番(2)(3):グループ内変化の群数列、分子で場合分け
(2)、小問がある種の誘導になっており、それを書いて整理→規則を発見できればクリアできる問題でした。
(3)は分子ごとに分けて考える判断ができれば、後は書き出しても短時間で処理できる問題でした。
■5番(3):誘導、(1)の利用、×=×の逆比
どう処理していくかがやや難しい問題でしたが、(1)での差に着目に気づくことが出来れば、あとは×=×の逆比で処理しておしまいでした。
小問が多い問題においては誘導を疑う意識は持っておきましょう。
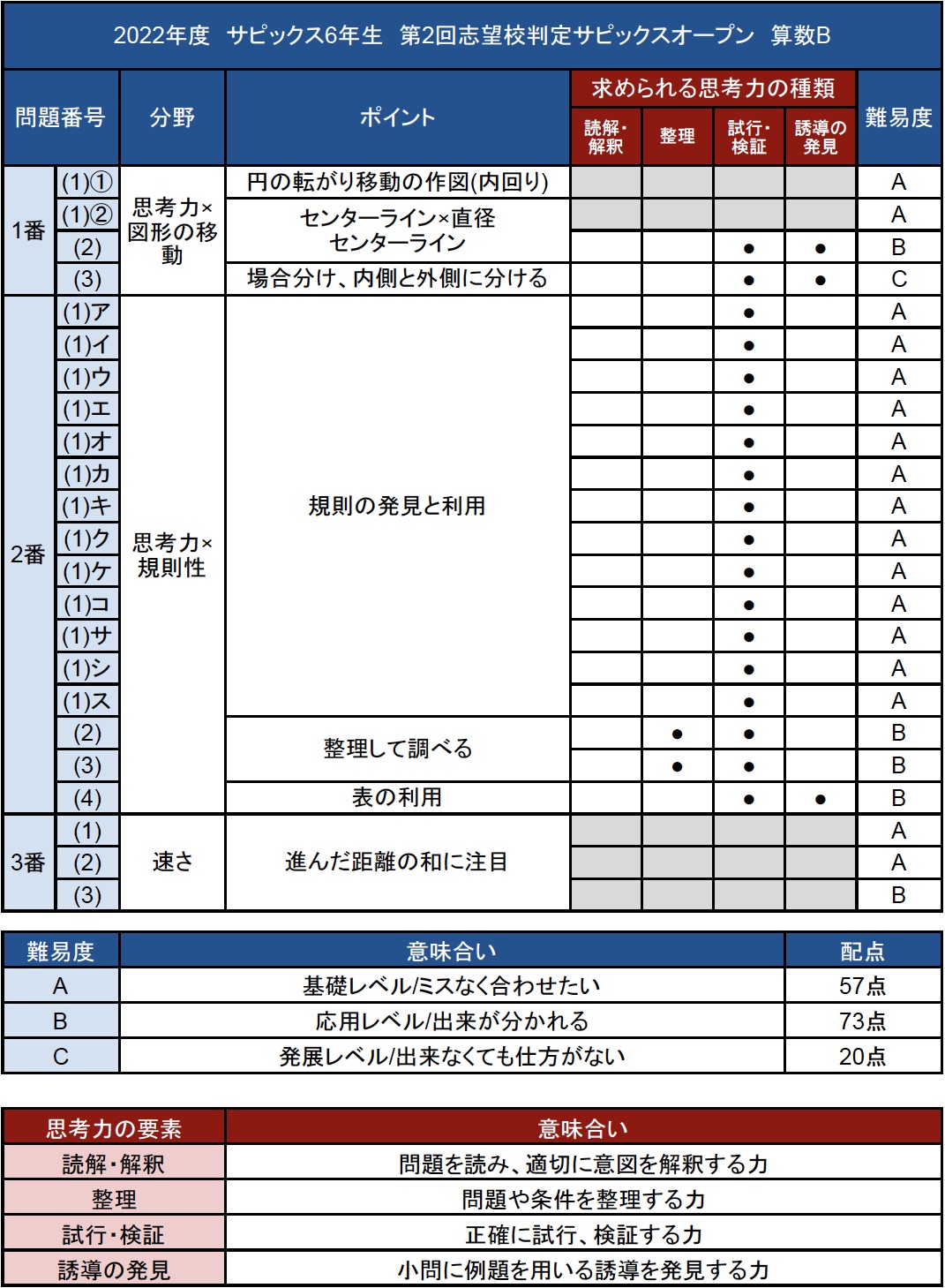
<算数B>第2回志望校判定サピックスオープンの難易度・所感
第2回志望校判定サピックスオープン(SO)の【算数B】です。
全体感としてはレベルAが約4割、レベルBが約5割、残りがレベルCという相変わらず難易度の高いセットとなりました。
ただし、大問2番と大問3番については着想や発想の斬新さや鮮やかさなどは要求されておらず、緻密に調べていきながら検証して進んでいくことで、やや時間はかかるものの答えにたどり着きやすい問題だったかと思います。
以下、レベル B以上の問題に対してコメントしておきます。
■1番(2)(3):センターライン×直径、センターライン、場合分け、内側と外側に分ける
(2)(3)は(1)を通じて学んだことを活かして場合分けを行うことが鍵でした。
その上で、(2)はセンターラインの公式を用いて式を組み立てると、短時間で答えに到達することが出来ます。
(3)は中央部分の差が分かるのでそれを活かした上で解いていく難易度の高い問題でした。
■2番(2)(3)(4):整理して調べる、表の利用
アプローチは分かり易いものの緻密に調べていくところでミスを誘発しやすいタイプの問題でした。
(1)で間違えてしまうとそれ以降の問題にも影響するという仕掛けになっており、前の小問ほど慎重に解いていくことも意識しておいて欲しい問題です。
■3番(3):進んだ距離の和に注目
思考力というよりも技術系の問題で、場合分けが入るもののその場合分けも決して発想しにくいものではない為、正解が狙いやすいタイプの問題だったかと思います。
尚、思考力の伸ばし方については、以下の記事をご覧下さい。
この記事では、中学受験算数で大切になる「思考力」とは何か? 近年のトレンドと学校別の思考力のパターン、そしてその伸ばし方についてお話しいたします。時に、思考力は「地頭」とほぼ同一のものとして語られます。「思考力を伸ばす」と[…]
第2回志望校判定サピックスオープンの算数解説動画
今回の記事では、第2回志望校判定サピックスオープンの解説動画を配信させて頂き、 分からなかった問題の解消にお役立て頂くことを目的としております。
ただし、算数Aの5~6番・算数Bの1番と3番は、StandByメンバー様との公平性の観点よりご意見を頂きましたため、大変申し訳ございませんが、メンバー様限定とさせていただきます。是非無料体験登録の上、ご覧ください。
※テストが実施された当月か、翌月に無料体験を申込まれた方は、無料体験内容にこのテストは含まれます。また、サピックステキスト解説と併せてご購入いただくこともできますし、このテスト解説だけをご購入いただくこともできます。(2022年受験組に限る)

〜算数A〜
1番(1)
1番(2)
1番(3)
2番(1)
2番(2)
2番(3)
2番(4)
2番(5)
3番(1)
3番(2)
3番(3)
3番(4)
3番(5)
4番
〜算数B〜
2番
算数Aの5~6番・算数Bの1番と3番は
コベツバからのお知らせ(コベツバWeb授業)
コベツバでは、「中学受験算数で必要になる土台となる技術を体系的に復習したい」「(難関入試に必要とされる)思考力を伸ばしていきたい」というお子様に向けて、コベツバWeb授業を配信しております。
分野別に分かれた教材・確認テスト(順位・表彰付き)や、毎週2問ずつ思考力を求められるテストを配信しております。
コベツバWeb授業の使い方につきましては、以下の記事をご参考下さい。
講座の概要と、あなたにぴったりの利用法を見つけよう!学年や利用目的に応じたあなたにぴったりのコースを診断の上で、コベツバweb授業の内容と活用法をご紹介いたします。コベツバ成長コース / 塾の算数強化コース / 塾の先取りコース […]
