公開中!
- 徹底分析:過去10年超の蓄積データから、難易度・傾向変化を紐解きます。
- 算数解説動画:正解への最短ルートを動画で伝授!
- 入試基本データ:偏差値・受験者数・最低点などを総ざらい。
- 来年度に向けた対策:中受算数のプロが示す、合格へのロードマップ。
・卒業生の正答率データと”合格処方箋”で「今やるべきことと現在地」がわかる
2026年東邦大学付属東邦中学入試の基本データ
東邦大学付属東邦中学の偏差値(サピックス/四谷大塚/日能研)
前期
| サピックス80% | サピックス50% | 四谷大塚 | 日能研 | |
| 2026 | – | – | – | – |
| 2025 | 54 | 48 | 61 | 63 |
| 2024 | 53 | – | 男 61 女 64 | 62 |
| 2023 | 54 | – | 男 61 女 64 | 男 62 女 63 |
| 2022 | 55 | – | 男 61 女 64 | 男 60 女 62 |
| 2021 | 55 | – | 男 61 女 64 | 男 60 女 62 |
| 2020 | 55 | – | 男 61 女 64 | 61 |
後期
| サピックス80% | サピックス50% | 四谷大塚 | 日能研 | |
2026 | – | – | – | – |
| 2025 | 55 | 52 | 60 | 61 |
| 2024 | 55 | – | 男 60 女 62 | 61 |
| 2023 | 55 | – | 男 60 女 62 | 61 |
| 2022 | 55 | – | 男 61 女 64 | 男 60 女 62 |
| 2021 | 55 | – | 男 60 女 62 | 62 |
| 2020 | 56 | – | – | 63 |
東邦大学付属東邦中学の受験者・合格者数・受験倍率推移
前期
| 受験者 | 合格者 | 倍率 | |
| 2026 | – | – | – |
| 2025 | 2195 | 967 | 2.27 |
| 2024 | 男 1339 女 804 | 男 648 女 324 | 2.20 |
| 2023 | 男 1329 女 818 | 男 632 女 335 | 2.22 |
| 2022 | 男 1331 女 795 | 男 639 女 330 | 2.19 |
| 2021 | 男 1384 女 874 | 男 630 女 324 | 2.27 |
| 2020 | 男 1492 女 900 | 男 707 女 304 | 2.37 |
| 2019 | 男 1481 女 929 | 男 642 女 324 | 2.49 |
| 2018 | 男 1447 女 849 | 男 662 女 416 | 2.13 |
| 2017 | 男 1421 女 911 | 男 673 女 439 | 2.10 |
後期
| 受験者 | 合格者 | 倍率 | |
| 2026 | – | – | – |
| 2025 | 297 | 38 | 7.82 |
| 2024 | 男 186 女 159 | 男 9 女 11 | 17.25 |
| 2023 | 男 235 女 222 | 男 11 女 11 | 20.77 |
| 2022 | 男 220 女 177 | 男 23 女 24 | 8.45 |
| 2021 | 男 215 女 164 | 男 11 女 10 | 18.05 |
| 2020 | 男 275 女 236 | 男 19 女 14 | 15.48 |
| 2019 | 男 214 女 208 | 男 32 女 34 | 6.39 |
| 2018 | 男 266 女 186 | 男 13 女 9 | 20.55 |
| 2017 | 男 250 女 187 | 男 13 女 12 | 17.48 |
東邦大学付属東邦中学の合格最低点・受験者平均点
前期【4科目】
| 合格最低点 | 受験者平均 | |
| 平均 | 259.1(65%) | 248.8(62%) |
| 2026 | – | – |
| 2025 | 255 | 242.4 |
| 2024 | 264 | 252.8 |
| 2023 | 278 | 268.8 |
| 2022 | 246 | 237.8 |
| 2021 | 263 | 252.6 |
| 2020 | 249 | 236.8 |
| 2019 | 251 | 239.9 |
| 2018 | 259 | 250 |
| 2017 | 267 | 258 |
前期【算数】
| 受験者平均 | |
| 平均 | 57.1(57%) |
| 2026 | – |
| 2025 | 54.8 |
| 2024 | 69.3 |
| 2023 | 71.8 |
| 2022 | 65.9 |
| 2021 | 42.0 |
| 2020 | 52.3 |
| 2019 | 45.1 |
| 2018 | 47.3 |
| 2017 | 65.5 |
後期【4科目】
| 合格最低点 | 受験者平均 | |
| 平均 | 224.7(75%) | 185.1(62%) |
| 2026 | – | – |
| 2025 | 205 | 177.7 |
| 2024 | 231 | 188.6 |
| 2023 | 237 | 193.6 |
| 2022 | 179 | 146.4 |
| 2021 | 245 | 199.4 |
| 2020 | 231 | 186.5 |
| 2019 | 233 | 203.5 |
| 2018 | 241 | 196.6 |
| 2017 | 220 | 173.6 |
後期【算数】
| 受験者平均 | |
| 平均 | 61.6(62%) |
| 2026 | – |
| 2025 | 60.4 |
| 2024 | 64.9 |
| 2023 | 68.0 |
| 2022 | 45.5 |
| 2021 | 61.3 |
| 2020 | 64.4 |
| 2019 | 70.0 |
| 2018 | 68.4 |
| 2017 | 51.4 |
東邦大学付属東邦中学の科目別配点と試験時間
前期
| 点数 | 制限時間 | |
| 国語 | 100点 | 45分 |
| 算数 | 100点 | 45分 |
| 理科 | 100点 | 45分 |
| 社会 | 100点 | 45分 |
後期
| 点数 | 制限時間 | |
| 国語 | 100点 | 45分 |
| 算数 | 100点 | 45分 |
| 理科 | 50点 | 30分 |
| 社会 | 50点 | 30分 |
2026年東邦大学付属東邦中学入学試験(前期)の算数
東邦大学付属東邦中入試(前期) 算数の問題PDF
東邦大学付属東邦中入試(前期) 入試の振り返り
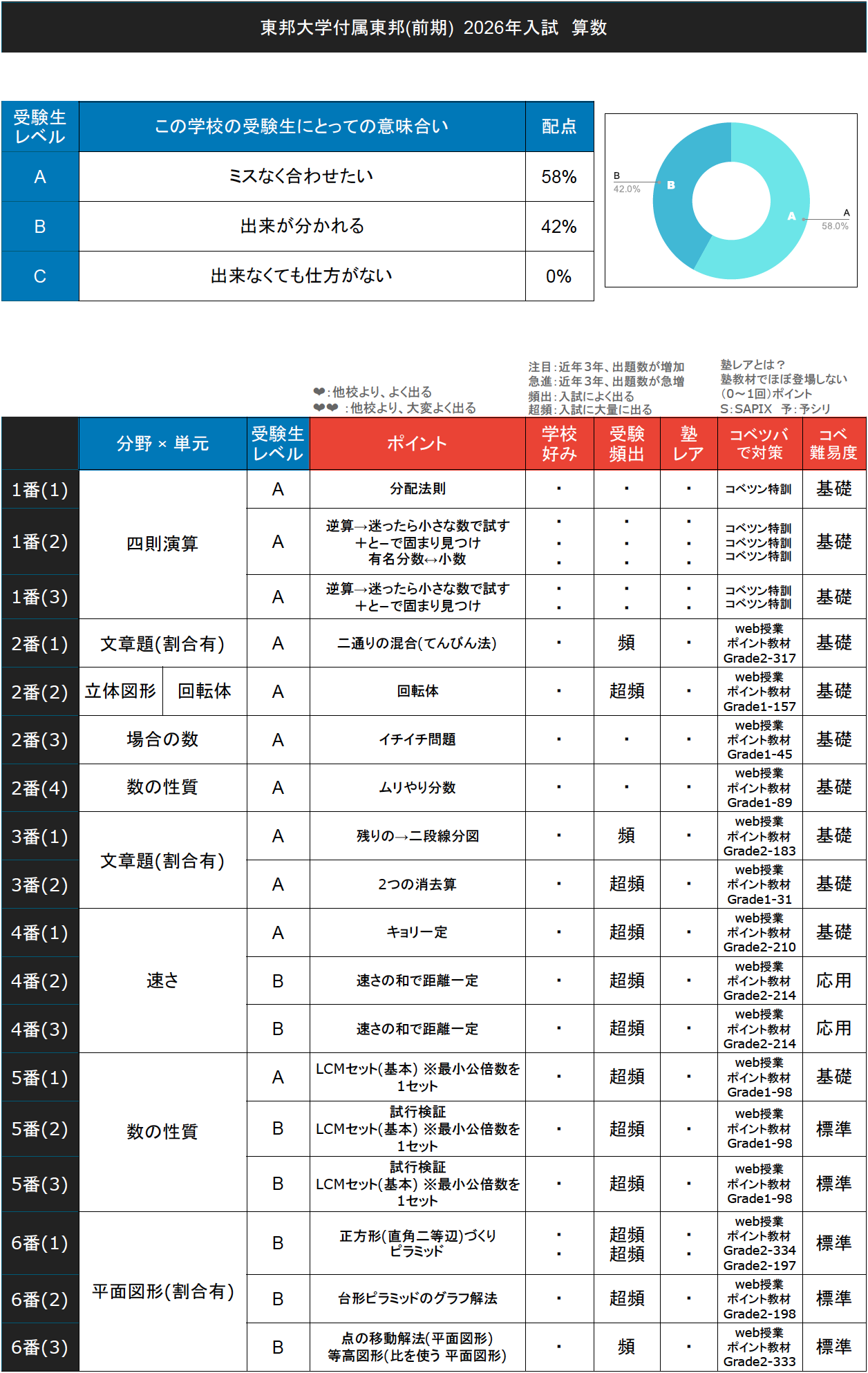
2026年、東邦大学付属東邦中の前期入試でした。
全体感を見ていくと、レベルAが約58%、残りがレベルBの約42%というやや難し目の構成となりました。
全問が技術系でありながら、4番は応用的な技術の使い方を問いかける古典的な問題、5番は遠距離から技術だけで解決できずに検証を入れる姿勢・判断をとることができるかが問われた問題、6番は同年の灘中1日目でも出題された直角二等辺づくりの問題でした。
全問が技術系で構成されており、受験生にとっても全く初めてという感覚を持つ問題ではないはずなので、これまで出会ってきた論点をどこまで1つ1つどこまで身につけてきたかで決まったのではないかと想像されます。
以下、レベルBの問題に対してコメントしておきます。
■4番(2)(3):速さの和で距離一定
(1)で速さの比が出ます。
1回目の出会いから2回目の出会いまでの時間とは、2人の速さの和で一周するのと同じ時間です。
従って、AとA+Bで一周のキョリ一定をかけて解くことができます。
■5番(2)(3):試行検証、LCMセット(基本) ※最小公倍数を1セット
(2)、12の倍数+6を120まで調べれば終わりです。
この「調べればそれほど時間をかけずに終わり」という判断ができるかが鍵でした。
Cだけ=(2)で消したものと、Dだけ12の倍数を120まで調べて判断すると求めることができます。
■6番(1)(2)(3):正方形(直角二等辺)づくり、ピラミッド、台形ピラミッドのグラフ解法、点の移動解法(平面図形)、等高図形(比を使う 平面図形)
直角と45度なので復元した上で、直角二等辺の片側に直角三角形が付いているので直角二等辺づくりという判断ができるかどうかが全てでした。
東邦大学付属東邦中入試(前期) 今年の一題にチャレンジ!
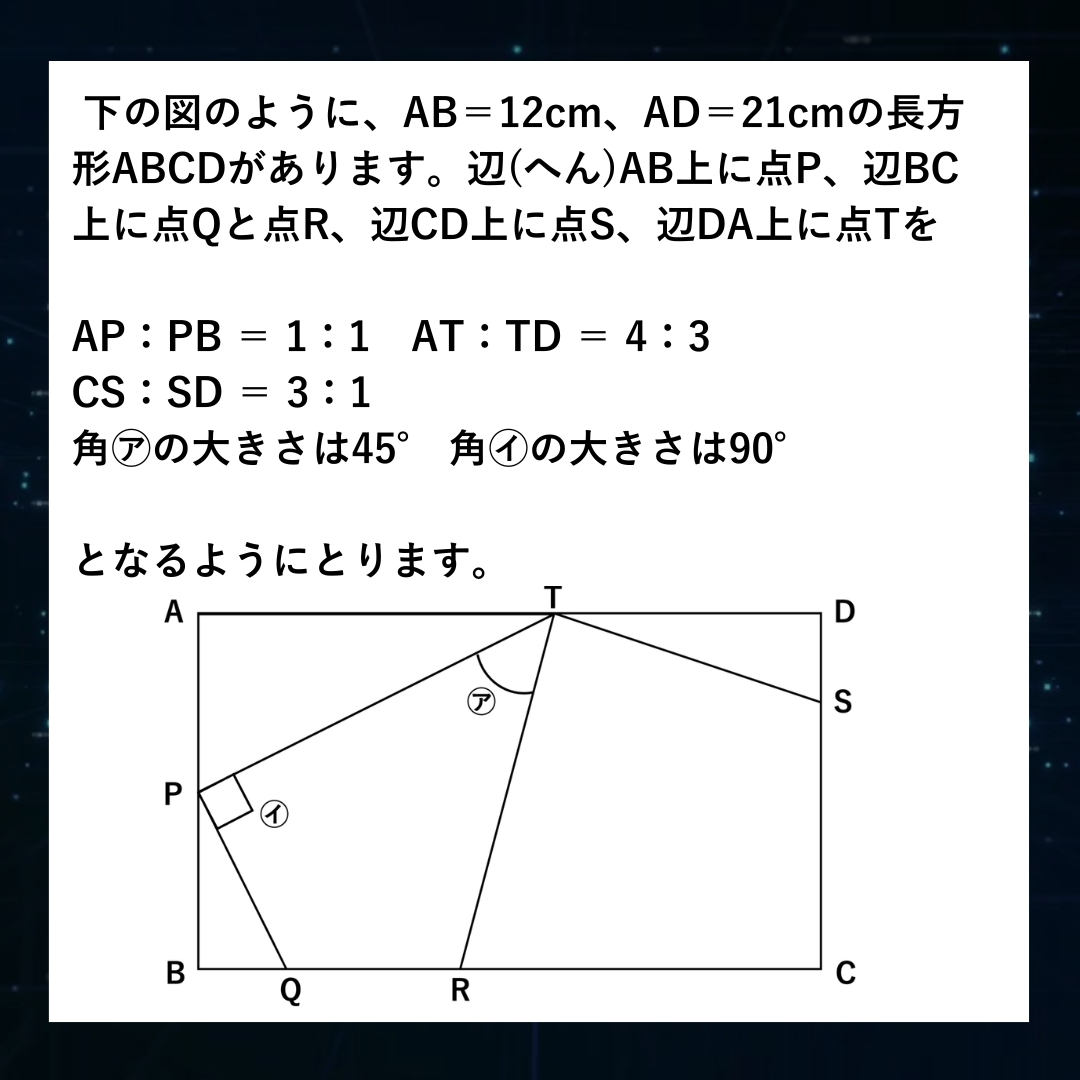

6番
【注意】解法に関するご質問やご意見
ご質問やご意見は以下のメールアドレスまでお問い合わせ下さい。
contact-us@chugakujyuken.kobetsuba.jp
学校の迷惑となりますので、学校へのお問い合わせはしないで下さい。
東邦大学付属東邦中学志望者向け 来年度に向けた対策
以下の2点を対策しておくことが望まれます。
■1.基本技術の典型問題の網羅
2026年は、これまでの頻出分野通りの出題となりましたが、2025年のように頻出以外の分野での出題が多くなる場合もあります。
従って、分野を絞って対策をする以上に、どの分野であっても基本問題は得点できる状態を目指すことがまず求められることになります。
■2.基本技術を用いた応用問題への対応力強化
2026年度の4番から6番で使う技術は、技術単体では多くの受験生にとってどこかで必ずといっていいほど学習したことがあるはずです。
ただ、その技術を用いた難易度がやや高い問題(コベツバの入試標準レベル)まで視野に入れて身につけておく必要があります。
受験生のレベルが高いために、頻出分野の基本レベルの問題では差がつかずに結局、技術は一般的でも捻られた問題でこそ差がついてくるためです。
