『筑波大学附属駒場中学入試の解体新書』とは?
筑駒中学の入試を解体・徹底分析し、一般の方からは非常に見えづらい入試および入試問題の特徴を明らかにすることを通じて、世間一般で言われている常識とは異なる考察をお伝えし、入試突破にあたっての体系的な指針を提供することを目的としております。
入試対策において「全ての科目、全ての分野、全てのポイントを対策すること」は時間と能力に余裕があればそれがベストです、でもそれはあくまでも理想論です。
現実は、時間との戦い・屈強なライバルたちの戦いであり、その為には、時間対効果が高いと考えられる勉強を入試突破に向けて戦略的に行う必要があります。
改めて丁寧に分析して判明したことは、筑波大学附属駒場中学は出題分野における偏りがあり、子供たちに求める能力も一貫しており、どの分野で合否を分けているかが推測できる学校と言えます。
まだ志望校対策に腰を据えて取り組む前段階である5年生や、追加の学習の余裕がない6年生前半でも、志望校を意識し、頻出単元の応用・発展技術には積極的に手を伸ばしていくことで、6年生後半の志望校別特訓クラスのスタート時点でライバルと数段の差をつけることもできるでしょう。筑駒突破の頂に向けて最短・最速で登って頂く為に、是非ご活用頂ければ幸いです。
音声版はこちらから!
筑波大学附属駒場中の最新入試の算数解説動画、難易度・傾向分析などは以下からご覧いただけます。
2025年入試の基本データ
筑波大学附属駒場中学偏差値(サピックス/四谷大塚/日能研)
| サピックス80% | サピックス50% | 四谷大塚 | 日能研 | |
| 2026 | – | – | – | – |
| 2025 | 71 | 67 | 74 | 72 |
| 2024 | 72 | – | 73 | 72 |
| 2023 | 72 | – | 74 | 72 |
| 2022 | 70 | – | 73 | 72 |
| 2021 | 70 | – | 73 | 72 |
| 2020 | 70 | – | 73 | 71 |
筑波大学附属駒場中学の受験者・合格者数・受験倍率推移
| 受験者 | 合格者 | 倍率 | |
| 2026 | – | – | – |
| 2025 | 532 | 131 | 4.1 |
| 2024 | 555 | 128 | 4.3 |
| 2023 | 521 | 128 | 4.1 |
| 2022 | 479 | 129 | 3.7 |
| 2021 | 561 | 131 | 4.3 |
| 2020 | 563 | 130 | 4.3 |
| 2019 | 624 | 129 | 4.8 |
| 2018 | 554 | 128 | 4.3 |
| 2017 | 591 | 127 | 4.7 |
| 2016 | 641 | 127 | 5.0 |
2022年度は3.7倍と低倍率となりましたが、2023年以降は再び4倍で推移しています。他の難関校が3倍程度で推移していることを考えると、2月3日校の筑駒は最高峰を目指す厳しい戦いであることが伺えます。
筑波大学附属駒場中学の合格最低点
【4科目】
| 合格最低点 | |
| 平均 | 340.6(68%) |
| 2026 | – |
| 2025 | 326 |
| 2024 | 353 |
| 2023 | 329 |
| 2022 | 358 |
| 2021 | 334 |
| 2020 | 340 |
| 2019 | 322 |
| 2018 | 344 |
| 2017 | 371 |
| 2016 | 329 |
4科目の総合点に、報告書100点分を加えた500点満点で、計算されます。
合格者平均点、受験者平均点はともに公表されておりません。
筑波大学附属駒場中学の科目別配点と試験時間
| 点数 | 制限時間 | |
| 国語 | 100点 | 40分 |
| 算数 | 100点 | 40分 |
| 理科 | 100点 | 40分 |
| 社会 | 100点 | 40分 |
配点は4科目均等に100点ずつと、報告書100点の合計500点となっています。報告書のどういった項目が評価されるかどうかは公式に明らかにされていないものの、試験科目ではない副教科の能力や、課外活動が評価されるそうです。
合格最低ラインは7割前後です。関東最難関の筑駒と比べると、関西最難関の「灘中」は算数配点が40%を占め、合格最低点が60%前後である学校で、灘は算数突き抜け型のお子様と相性のよい学校です。
しかし、筑駒は全く逆であり、算数だけが得点できたとしても合格が難しい学校であると言えるでしょう。
筑波大学附属駒場中学の算数概観
筑波大学附属駒場中学の算数 単元別出題比率
筑駒中の過去10年間の配点を推定・集計した入試問題の分野別出題シェアと出題比率のグラフは以下のようになります。(なお、正確な配点は公表されていないため、あくまでも推定値での算出となります)
出題得点シェアが高い順に
このようになっており、これら主要5分野で9割近い得点を占めています。
一目で明らかなほど偏っており、例えば開成で最も出題されるようなピュアな速さの問題はほとんど出題されていません。代わりに、速さの考え方が図形的な要素とミックスされた、図形・点の移動や水槽の問題といった特殊な問われ方の問題が出題されます。
また、場合の数や規則性の問題といった、受験生に手を動かして実験させる問題も多い傾向にあります。
筑波大学附属駒場中学の算数 難易度比較
筑駒の問題は開成と比べて簡単なものが多い?
過去10年間で出題された問題を難易度レベル別で分けると、以下のような比率になります。
A=筑駒受験者の大半が正答できる問題
B=筑駒受験者の中で、正答できるかどうかが分かれる問題
C=筑駒合格者でも出来ていない人が多いと思われる問題
となり、開成と比較すると少しレベルCが減少し、レベルAが増加しています。
筑駒は科目別の合格者データが公表されておらず、調査書の100点の内訳が不明瞭となっているものの、全科目における合格最低点のボーダーは70%前後となっています。
年度によりますが、開成においても算数の合格ラインは70%前後であることを考慮すると、「なんだ、筑駒の方が簡単なんだな」と思えるかもしれません。
しかし、実はこの考え方には大きな誤りがあります。
開成が60分で大問3〜4題構成であるのに対し、筑駒は40分で大問4題構成となっているためです。
筑駒の算数は開成の算数と比べて『一問の量がハードで、問題の理解が難しい』ということが少なく、開成とはメインに出る分野も異なれば、同じ分野でも出し方が異なってきます。問題文が長く熟考を要する開成と、短い時間内でスピーディーな処理を求められる筑駒とでは毛色が異なっており、受験生自身にもかなり向き不向きが出やすく、どちらが高得点を取りやすいかは得意単元や個人の性格で変化します。ただ、正しい訓練を積むことによってある程度慣れてくれば、どちらも得点できるようになっていきます。
このように、筑駒の受験においては、「限られた時間をいかに有効に使うか」が非常に重要です。レベルAとBで90%近くを占めるということは、たとえCが正答できずとも、Aを全て正答し、Bを半分以上正答すれば十分合格可能であるということを示しています。
筑波大学附属駒場中学の算数 難易度×単元比率
ここまでで頻出単元と難易度の比率を示したわけですが、単元毎の難易度が気になるところです。
では、難易度レベル毎の出題単元のシェアを見ていきます。
まず、「レベルA=筑駒受験者の大半が正答できる問題」です。
出題割合に対して、規則性や数の性質の問題中にレベルAの問題が多くを占めることがわかります。
次に「レベルB=筑駒受験者の中で、正答できるかどうかが分かれる問題」です。
場合の数の割合が高く、簡単過ぎず、難し過ぎずといった形で、合否に直結しそうな分野が顔を揃えています。
最後に「レベルC=筑駒合格者でも出来ていない人が多いと思われる問題」です。
レベルCは、一部の算数が得意な受験生を除き、問題に時間をかけたところで解けるかどうかが怪しい問題です。他のレベルA Bを解き切っていないのにも関わらずレベルCを解こうとするのは無謀と言えます。「レベルCだ」と感じたら一旦離れるのも懸命な判断でしょう。
●「明暗を分ける難易度Aの問題をミスなく得点したい、でもどうしても苦手な分野がある…!」こんな悩みは筑波大附属駒場中学志望のお子様につきものです。中学受験コベツバでは、このような苦手分野に効果的にアプローチする解説動画配信サービスを提供しております。
平面図形の出題割合は全体の15%に過ぎなかったことを考えると、レベルCにおいて圧倒的なシェアを誇っていることが伺えます。
これはつまり、平面図形の大問の終盤は非常に難解な問題である場合が多いということであり、あまり悩んで時間をかけ過ぎてしまうと泥沼にはまってしまう恐れがあるということです。
平面図形の問題は、視覚的には理解しやすい分、「これは解けそうだ!」と思ってしまう生徒が多いため、要注意です。
一方で、規則性や場合の数は、出題数の割にレベルCが少ないという特徴があります。これは単元の性質上、
(1)実験
(2)規則を見つける
(3)規則の利用(2020回目は〜といったもの)
というパターンが多く、(3)でいきなり難問になるといった状況が少ないからということも考えられます。
図形・点の移動においては、単純に終盤の作業量が多く、時間を要することがあります。そういう面で時間内に解き切ることが難しい場合があるので、「かける時間に見合った点数が手に入るか」「今これを解くのが最善なのか」ということを常に意識したいところです。
以上を踏まえた上で、基本的に重要なのは「難しくて解けないC問題に時間をかけないこと」であり、その分の時間でAB問題を解き切るようにする必要があります。そして、平面図形の終盤は難解なことが多く、規則性や場合の数は比較的容易なものが多いということも分かりました。
筑波大学附属駒場中学の算数全般的な対策
時間の使い方
時間を大切にする人が筑駒算数を制する!
筑駒はかなり時間にルーズでマイペースな生徒が多いというのが専らの評判ですが(卒業生談)、実は、入試に関しては真逆の超短期決戦型といえます。
普段マイペースに好奇心を持って学習し、様々な問題に取り組みながら体系的に思考を深めていくことが大切である一方で、入試やテストに関しては「決められた時間で自分の得点を最大化するゲーム」だということを意識しましょう。
「難しい問題を解けた!」というのは素晴らしいことなのですが、入試ではたくさん正答を積みあげた人が合格していくわけなので、むしろ「易しい問題をできる限りたくさん正答する」ことの方が重要になってきます。
筑駒の時間の戦いを制するには、
1:計算力や処理能力の向上といった瞬発力を磨くこと
2:テクニックや整理方法を鉄壁まで身につけ、迷いをなくすこと
3:実際の入試においては、作戦を立てること
この3つのポイントがあります。
筑駒の算数は時間をかければ、他の難関校受験生でも十分に解くことができますが、「1:処理能力」や「2:テクニック」を高めていることで制限時間内に問題を解き切ることができるのです。この「1:処理能力」や「2:テクニック」は、直前期に急に能力が上がることはありませんから低学年から鍛え続けて欲しい能力です。低学年の頃から難しいポイントでも怯まずにテクニックをストレスなく技術を使えるように身に付けましょう。そして「正解した」ことで満足せずに、「もっとスマートに解けなかったのか?」と振り返り、模範解答や講師の書き込みなどから「どうやったらスマートに整理・処理できるのか」を真似ていくことで鍛えておいて欲しいところです。
3の「作戦」については、1,2を磨いた上で直前期にフォーカスしていきましょう。
「作戦」についてもう少し詳しくお話いたします。
3章で触れた通り、筑駒の得点の目安は70%であり、算数で差をつけたいならば75-80%を得点しなければなりません。
そのためにもA問題を全て正答し、B問題を半分以上正答した上で、C問題にできるだけ時間をかけないことが基本戦略になります。
具体的に言うと、筑駒の算数は40分で大問4題構成です。つまり、1つの大問にかけられる時間はたったの10分しかありません。
大問に15分や20分かけて解けたところで、それに圧迫されて他の大問が解けなければ大惨事が待ち受けています。
そのため、試験時間を意識して、もし一つの大問に10分以上かける場合は、他の問題を終わらせられるのかを確認するようにしましょう。
そして、答えを合わせる目処が立っていない場合、見直しを優先しましょう。ある大問で(1)からケアレスミスしてしまっていた時点で、合格は相当遠ざかってしまいます。
それでは、具体的に「解くべき、優先するべき場所」というのはどこなのでしょうか?
1つの大問は3-4問から構成されているので、仮に全ての大問が3問構成だとすると、(1)(2)を全て合わせるだけで全体の67%になり、そこから解けそうな問題の(3)を1つ解くだけで75%、2つ解ければ83%に達します。下のように得点できればおよそ75%となります。
| (1) | (2) | (3) | |
|---|---|---|---|
| 大問1 | ○ | ○ | × |
| 大問2 | ○ | ○ | ○ |
| 大問3 | ○ | ○ | × |
| 大問4 | ○ | ○ | × |
このように得点するための模範的な試験時間40分の過ごし方は、以下のようになります。
1: 0-1分全ての問題をざっと見て、問題構成を把握する(この大問は規則性だな、問題文が長めだなといった程度で良い),解く順番を決める(推奨、後述)
2: 1-30分 全ての大問を上限8分として取り組んでみる。(分からない(3)はすぐ飛ばしたり、容易ですぐ終わるものがあったりするので、32分もかからないことが多い。)
3: 30-39分 解けていない(1)(2)があればそれを解き、見直していない(1)(2)があれば見直す。その後、残った(3)のうち、解けそうなものに取り組む。
4: (39-40分 場合の数などの白紙の答案にはそれらしい数値を書き込む)
この戦略には3つのポイントがあります。
1: 問題全体の構成を把握する
2: 制限時間を設定し、時間内に分からない問題はとりあえず一旦諦める。(2分程度かけて解法が全く思いつかない、または時間がかかりそうなら迷わず一旦捨てて次に行きましょう。)
3: 見直しをして、確実に(1)(2)を正答する。
もちろん、既に自分の中のルーティーンを確立している方は必ずしも真似る必要はないですが、一度試してみる価値はあるかと思います。
全分野に共通した考え方
各問の繋がりを意識する!
問題を解く際は、必ず「最初に(1)-(3)に目を通す」ことを習慣化します。慣れていくと一目でどれくらいのボリュームがあるかを推測することが出来ますし、これからどういうことを質問をされるのかということを認識した上で解法を選択することができます。(例えば、「(3)で2020回目とかを聞かれていたならば、(1)や(2)で何かしらの規則性を見つけておかなければならないな」といった形です。)
また、「(1)は(2)(3)のヒント(誘導)である」ということを理解しておく必要があります。
(2)や(3)で詰まった際は、まず、未使用の条件が問題文にないか振り返った上で、それ以前の問題が何のために存在したのかを考えてみましょう。そうすることで、作問者から提示されているヒントを読み取れる場合が多いです。
筑駒H16の大問2、平面図形の問題は非常に優れた問題で、(1)が設定されていなければ(2)(3)を大半の人が解けないでしょう。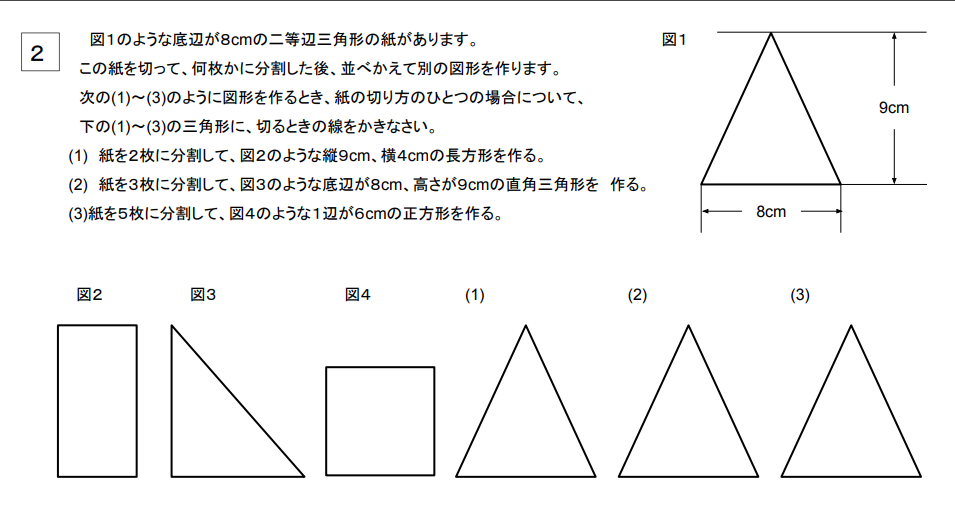 また、筑駒の(1)は簡単に設定されているためレアケースではありますが、(1)が解けなかったとしても、(2)(3)が解ける場合があります。そういう隙を逃さないためにも、前もって(1)-(3)に目を通しておくことを推奨します。
また、筑駒の(1)は簡単に設定されているためレアケースではありますが、(1)が解けなかったとしても、(2)(3)が解ける場合があります。そういう隙を逃さないためにも、前もって(1)-(3)に目を通しておくことを推奨します。
解く順番を決める
あまり算数で実行している人はいませんが、国語であれば物語文と説明文の解く順番などを自己設定している方も多いと思います。
「テスト時間が半分過ぎた…でも答案が半分も埋まってない…!!」
こんな時は、非常に焦りますね。
そのため、得意な順、時間がかかりにくい順、あるいは解法が分かりきっている順などなど、自分で基準を設定して順番通りに解くことを推奨します。
筑駒に関しては、早めに解くことを推奨したい分野が2つあります。
1: 規則性
→どの問題でも、 操作が決まっているため解きやすいが、終盤に持ち越してしまうと時間が足りなくなってしまう場合があります。
例えば速さなどの分野は、ダイヤグラムを使うか、線分図、比を使うか、といった解法選択の分岐が存在しますが、規則性に関しては「実験して表などでまとめることで規則を見つける」というように、操作が決まっているため取り組みやすい上に、筑駒では頻出です。
2: 平面図形
→解ける場合はすぐ解けて、解法が思いつかないときは時間をかけても思いつかないことが多いです。前者の場合はもちろん、後者の場合も(2)まで解いて、すぐに他の大問に移れば時間的なロスが少なく済みます。また、一旦諦めたとしても、最初のうちに取り組んでおけば、他の問題を解いている間にふと思いつく場合もあります。
他校の算数との類似点
ここまでで何度か述べていますが、偏差値帯が近いと言っても、開成の算数とは求められている能力が異なっています。
むしろ、開成というよりも灘の算数(1日目)と類似しています。筑駒は大問構成なのに対して、灘の算数(1日目)は小問集合という点で異なっていますが、「処理速度が求められるテスト」という観点では共通していると言えるでしょう。
また、分野的に見ると「場合の数」と「数の性質」で灘や甲陽学院(どちらも関西)に似たようなものが出題されていることがあります。
首都圏での受験を考えている方は見過ごしがちですが、関西の学校、特に灘の過去問演習をこなすことは、筑駒の入試での得点率を大きく上げることに繋がります。
筑波大学附属駒場中の算数分野別対策
場合の数
過去10年で最も出題配分が大きい分野です。
場合の数は大きく分けて下のような解法パターンがあります。
| 場合の数 | |
|---|---|
| 書き出す | 調べ上げ |
| 樹形図 | |
| 対戦表 | |
| 計算 | 組み合わせ |
| 順列 | |
書き出しのパターンでは「漏れなく、被りなく」ということを意識しましょう。また、書き出し始める前に下処理をすることで、書き出す個数を減らすことができます。
筑駒では、開成よりも1問あたりに費やせる時間が少ないため、書き出す個数が50個や100個になることはあまりありません。工夫することで少なく済ませたり、規則性や計算を利用して操作を省略することができます。
2014年大問4(2):

規則性
規則性は他の分野と比べて、解法の手順がほぼ固定されています。
(1)で実験→書き出す、表にする→規則(または例外)を見つける→利用する
実験についてはバリエーションがありますが、問題の誘導に沿って行えば、筑駒の(1)は簡単であることが多いので問題ないでしょう。
筑駒の規則性については、このように型が決まっているので過去問演習数年分を通じて素早く解く力を身につけるようにしましょう。筑駒が挑戦枠のお子様も、筑駒を目指せるレベルのお子様であれば「筑駒の規則性」は訓練さえすれば必ず得点できるようになります。
算数が苦手な受験生の方にはぜひ対策・得点源としてほしい分野です。
尚、規則についてはさまざまなパターンがあります。周期、等比、等差数列、2乗を繰り返すパターン、三角数のパターン…といった、様々な周期の問題を解いて「整理→規則の発見」までがスムーズに進むように準備しておきましょう。
2014年大問1(1):

●筑駒特有の規則性の発見問題については、こちらのサービスのNO16「規則性(2)」のテーマです。筑駒の過去問も多数掲載しており、筑駒志望者の規則性の攻略教材として有効です。
●最難関志望校別動画特訓「TopGun特訓」
図形・点の移動
昔ほどではありませんが、それでも筑駒では非常に出題頻度が高いです。
点の移動といっても、実は「1つの分野と呼んで良いのか?」というほど多彩なパターンがあります。
1: 図形的に解く
面積、形状を問われることが多いです。移動時間が短いとき(30秒など)は、書き出しをすることもあります。
2: 速さで解く
位置や動いた長さを問われることが多いです。点が図形の周上を回っていますが、池の周りを複数人が走っている問題と同じような形です。移動時間は短いことも長いこともあります。
3: 周期で解く
頂点にいる時や重なる時の時間などを問われることが多いです。移動時間は長めの場合があります。(2020秒後、など)
また、どの問題であっても、点の移動の問題や水槽の問題に共通して言えるポイントは「変化の節目を考える」ことです。
2012年大問1(2):
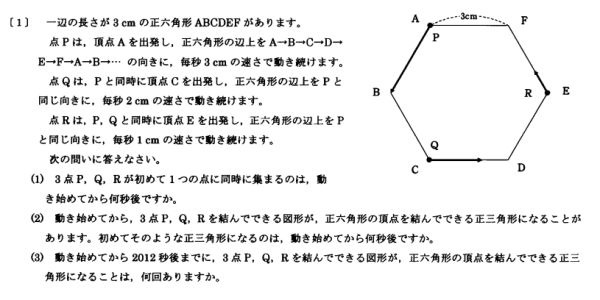
平面図形
平面図形にも様々なパターンがあります。
解法の選択の際は
1: 求積
1-1: 複雑な図形は分割するか、周りから引く。
1-2: 三角形の面積は、底辺×高さ÷2の公式の利用、面積比・相似比の利用などさまざまな求め方がある。
2: 角度
2-1: 有名角の場合は、150°,75°,60°,45°,30°などでは正三角形や正三角形の半分の利用を考え、108°などでは正多角形の利用を考える。
2-2: 具体値(27°など)の場合は外角や二等辺三角形、垂直、並行、合同、相似などを用いて計算する。
3: 円
円や弧を見つけた場合は中心に向かって線を引く。
4: 対称性
図形に対称性があれば、それを利用する。
5: 線分比
求めたい部分を含むような相似を作る。
といったように多岐に渡りますし、場合の数やパズルのような形で出題されることもあります。
2016年大問4
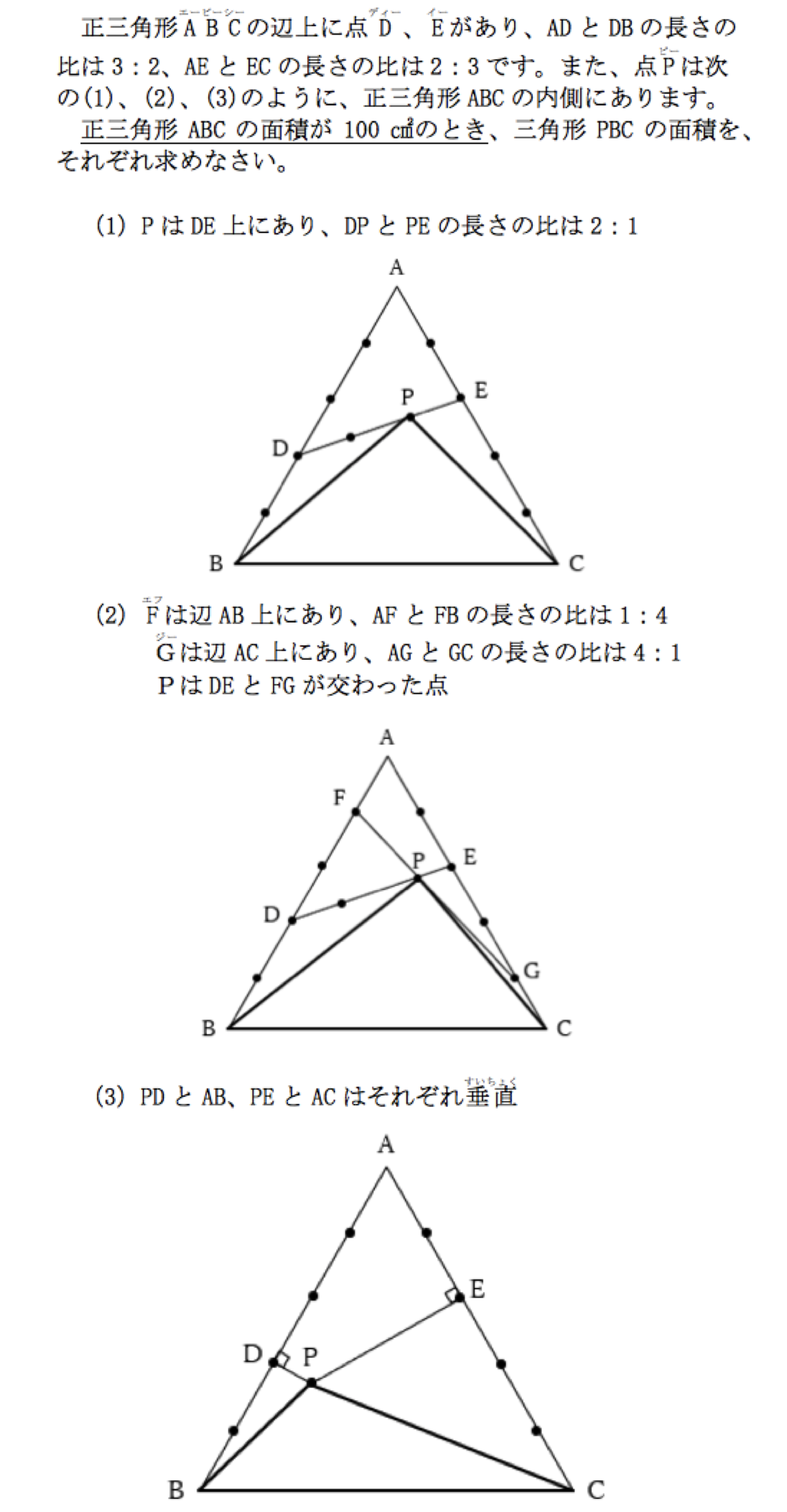
2018年大問4(2):
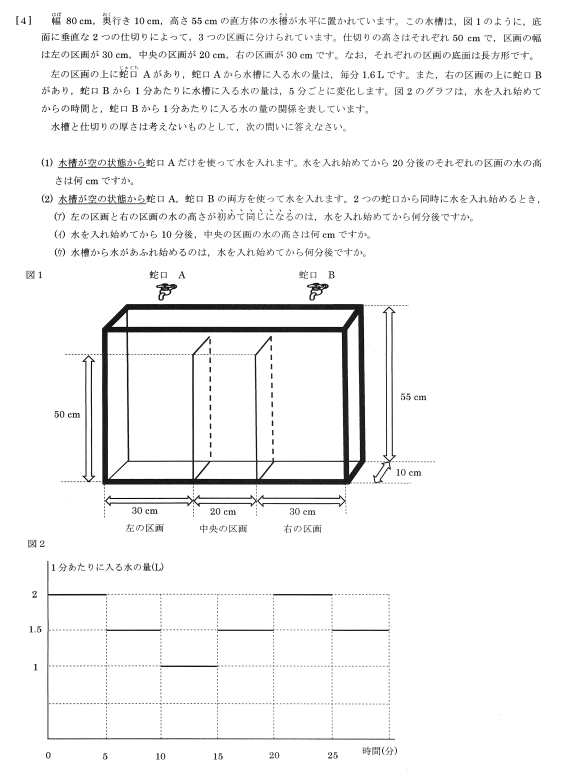
●近年難化が進み、差が付きやすい筑駒の平面図形ですが、先程もご紹介させて頂いたTopGun特訓NO9「平面図形(3)」で志望者の方が最低限知っておくと役に立つ筑駒頻出論点を取り上げています。(既に塾や市販教材でご存知のお子様もいらっしゃるかと思いますが。)








